A complete guide for extrapolation

Introduction

Suppose there is a farmer who daily observes the progress of crops in several weeks. He looks at growth rates and begins to reflect on how much higher than his plants could grow in other weeks. From the existing data, it makes an approximate forecast of additional increase. This operation of assuming the values ​​beyond the range of data points selected for the purpose is called extrapolation. But it must be said that farmers only need to understand extrapolation; Everyone who applies data analyzes for future -oriented purposes, whether a scientist or an engineer, should do so.

In this article, we will delve into the subject of extrapolation, discussing its need and the methods to do it.

Overview

• Understand the concept of extrapolation.
• Know different extrapolation methods.
• Recognizes the importance and extrapolation applications in various fields.
• Identify the limitations and challenges associated with extrapolation.
• Get information about best practices for precise extrapolation.

Extrapolation is a statistical method used to estimate or predict values ​​beyond a particular set of known data points. Expand the trends observed within the data to predict future results. Unlike the interpolation, which provides values ​​within the rank of known data, extrapolation companies in non -square territories, often carry higher risks and uncertainties.

Importance and extrapolation applications

Extrapolation plays a key role in various domains:

• Science and Engineering: Scientists apply the extrapolation procedure for predicting the results of the experiment and for understanding the operation of physical systems beyond the observed data.
• Finance: Entrepreneurs use market trends to invest and for the prediction of economic statistics through financial analysts.
• Weather forecast: Meteorologists also give details of the future weather pattern of analyzing the existing and previous data of the weather condition.
• Environmental studies: It can also be used to predict future change on ecosystems and to evaluate the effects of political measures on the physical world.

The extrapolation methods are varied, each with their unique approach to expand data trends beyond the known points. Here’s a more attentive look at some of the most used methods:

Linear extrapolation

Linear extrapolation is based on the assumption that the relationship between the variables is linear. If you have a set of data points that fall in a straight line, you can extend this line to predict future values.

Formula

y = mx + b

• (y): the expected value.
• (M): the slope of the line.
• (x): the independent variable.
• (b): The interception y.

Application

It is widely used when the data trend is consistent and shows no signs of curface or change of direction. For example, it is useful for the financial forecast where a price of actions can follow a trend up or down over time.

Advantages

• Simple to understand and implement.
• Effective for short -term predictions.

Disadvantage

• It can be incorrect if the data shows non -linear behavior over time.
• He assumes that the trend continues indefinitely, which may not be realistic.

Polynomial extrapolation

Polynomial extrapolation fits in a polynomial equation to data points. You can capture more complex relationships using higher -degree polynomials.

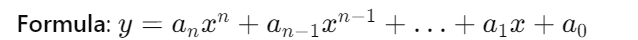
• (y): the expected value.
• (A_N): polynomial coefficients.
• (x): the independent variable.
• (N): The degree of the polynomial.

Application

Useful when the data shows curvature or fluctuating in a way that a straight line cannot represent. It is often used in scientific research where phenomena present non -linear behavior.

Advantages

• It can be adapted to a wide range of data trends.
• Greater flexibility in the modeling of complex relationships.

Disadvantage

• Increased risk of excess lace, especially with high -degree polynomials.
• More complex and computational intensive than linear extrapolation.

Exponential extrapolation

This method is used when the data grow or decay at an exponential rate. It is suitable for phenomena that increase or decrease rapidly.

• (y): the expected value.
• (a): the initial value (when (x = 0)).
• (B): The growth rate.
• (x): the independent variable.

Application

Used commonly used in population growth studies, radioactive decay and financial contexts where compound interest is involved.

Advantages

• Capture rapid growth or decay effectively.
• It offers good data adjustment with exponential trends.

Disadvantage

• It can lead to extreme values ​​if the growth rate (b) is large.
• It assumes a constant growth rate, which cannot always be accurate.

Logaritmic extrapolation

Logaritmic extrapolation is useful for data that rapidly grow at the beginning and then can be disabled. Use a logarithmic function to model data.

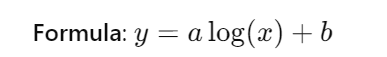
• (y): the expected value.
• (a): The coefficient that scores the logarithmic function.
• (x): the independent variable.
• (b): The interception y.

Application

It is often used in natural phenomena such as the rapid initial growth of populations or cooling hot objects, where the exchange rate decreases over time.

Advantages

• It is good to model data that rapidly increases at first and then stabilized.
• Less prone to extreme values ​​compared to exponential extrapolation.

Disadvantage

• Limited to data that follow a logarithmic trend.
• It may be less intuitive to understand and apply.

Extrapolation Average Moving

This method softens short -term fluctuations and highlights long -term trends by average data points during a specified period.

Process

• Select a window size (number of data points).
• Calculate the average of the data points within the window.
• Slide the window forward and repeat the process on average.

Application

Widely used in time series analysis, such as stock market trends, to reduce noise and focus on the global trend.

Advantages

• Softens short -term volatility.
• Help long -term trend identification.

Disadvantage

• It may be behind the real data trends.
• The choice of window size can significantly affect the results.

Examples of extrapolation

To better understand the application of different extrapolation methods, let’s consider some practical examples in various fields.

Stage: A company wants to predict its future sales based on historical data.

Historical data:

• Year 1: $ 50,000
• Year 2: $ 60,000
• Year 3: $ 70,000
• Year 4: $ 80,000

Sales increased by $ 10,000 each year, indicating a linear trend.

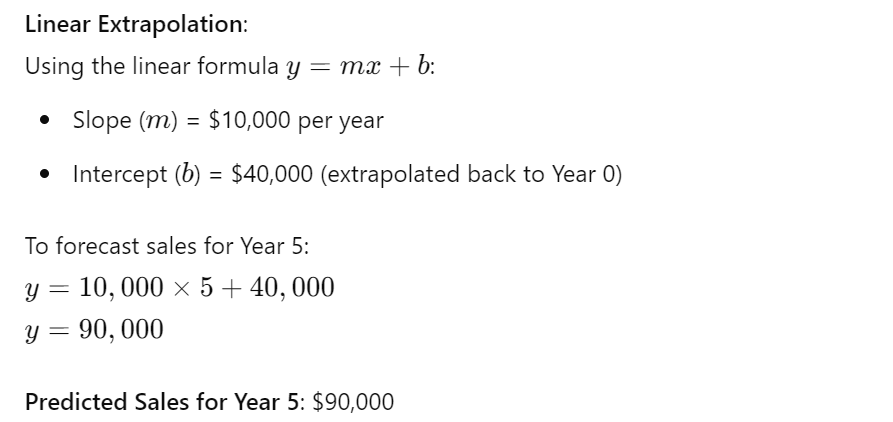
Stage: A biologist is studying the growth of a bacterial colony and warns that the growth rate is not linear but it follows a quadratic tendency.

Data:

• Time 1: 100 bacteria
• Time 2: 400 bacteria
• Time 3: 900 bacteria
• Time 4: 1600 bacteria

The relationship between time (x) and the population (y) seems to follow a quadratic equation (y = ax^2 + bx + c).

Stage: A researcher is tracking the spread of a viral infection and notes that the number of cases doubles each day.

Data:

• Day 1: 1 case
• Day 2: 2 cases
• Day 3: 4 cases
• Day 4: 8 cases

These data suggest exponential growth.

Stage: An engineer is studying the cooling rate of a heated object. The object cools quickly at first and then slower, following a logarithmic trend.

Data:

• Minute 1: 150 ° C.
• Minute 2: 100 ° C.
• Minute 3: 75 ° C.
• 4: 60 ° C.

Stage: An analyst wants to soften daily fluctuations in stock prices to identify a long -term trend.

Data (Last 5 days):

• Day 1: $ 150
• Day 2: $ 155
• Day 3: $ 160
• Day 4: $ 162
• Day 5: $ 165

Limitations and challenges

Although extrapolation is a powerful tool, it includes major risks:

• Uncertainty: The more you extrapolate your results, the greater the variability, that is, the less needed the results of the extrapolation.
• Assumptions: However, extrapolation has its setback, it means that past trends will continue this may not be true most of the time.
• Fitted: Using complicated models support the risk where the model builds noise more than the trend.
• Terms of limit: Other things that are absent in extrapolation models are the limitation and barriers of physical and natural systems.

• Understand the data: This means that once you have done the extrapolation, you must perform a complete analysis of the results arrived before extrapolation to understand the trends, as well as data patterns.
• Choose the appropriate model: Choose the model with the format that will work well with the nature of the data to be analyzed. It was seen that the simplest models are better from the point of view of the robustness.
• Validate the model: Keeping a part of the data, you should check the model output and make corrections with the other part of the information.
• Consider external factors: To avoid compromising the validity of these discoveries, there are other factors and limitations with respect to the study as it must be taken into account:
• Quantify uncertainty: Give statistical probabilities next to the extrapolated values ​​in order to have a prolonged range of possibility.

Conclusion

Regression analysis is a fundamental statistical method necessary for the estimation of future values ​​as a continuation of the current observed values. Despite the benefits that are evident in this approach in various fields, there are risks and inherent challenges that come with it as will be discussed below. Although there are many types of regression analysis, each with strengths and weaknesses, when appropriate methods are applied, the correct predictions can be reached. To the same extent, extrapolation, if applied properly, remains a valuable help for decision making and policy planning.

Frequent questions